قبل از شروع برنامه نویسی PLC، اجازه دهید برخی از مفاهیم اساسی در مورد برنامه PLC را توضیح دهم.
اگر از زمان اسکن PLC اطلاع دارید، می توانید شروع به بررسی نحوه عملکرد برنامه PLC کنید. منطق ترکیبی به شما درک اساسی از نحوه ترکیب دو حالت – درست و نادرست با منطق را می دهد. اصول اولیه برنامه نویسی PLC ترکیب منطق است. به همین دلیل است که منطق ترکیبی می تواند راهی عالی برای برنامه نویسی PLC باشد، از آنجایی که اصول منطق ترکیبی و برنامه نویسی PLC یکسان است.
منطق ورودی
برنامه PLC را می توان به دو بخش تقسیم کرد. قسمت اول قسمت دوم را کنترل می کند. بخش اول منطق ورودی نام دارد. منطق ورودی تابع برنامه PLC است. همانطور که کلمه می گوید منطق ورودی منطق برنامه شما است. اما منطق چیست؟ مهم است که بدانیم منطق چیست، زیرا برنامه PLC منطقی است. به بیان دقیق تر، برنامه PLC منطق دیجیتال است. در ریاضیات جبر بولی نامیده می شود.
در جبر بولی یا منطق دیجیتال، مقادیر می توانند تنها یکی از دو حالت باشند: درست یا نادرست. در PLC ها true یا false با 0 برای false و 1 برای true نمایش داده می شود. ریزپردازنده ها و کامپیوترها اینگونه کار می کنند. آنها با 0 و 1 کار می کنند و زمانی که پی ال سی را برنامه ریزی می کنیم باید به 0 و 1 فکر کنیم. ما هنگام برنامه نویسی یک PLC از جبر و منطق بولی استفاده می کنیم زیرا آن ها اینگونه عمل می کنند.
منطق با یک مثال در دنیای واقعی
با یک مثال در دنیای واقعی شروع کنیم، اجازه دهید دریابیم که منطق دیجیتال واقعاً چیست.
این مثال ساده یک لامپ و دو کلید خواهد بود. دو بخش ساده با یک چیز مهم مشترک: هر دو دارای دو حالت هستند. لامپ و کلیدها یا روشن یا خاموش هستند.
ما می توانیم لامپ و سوئیچ ها را به روش های مختلف وصل کنیم. این باعث می شود که سوئیچ ها و لامپ به روش های مختلف عمل کنند.
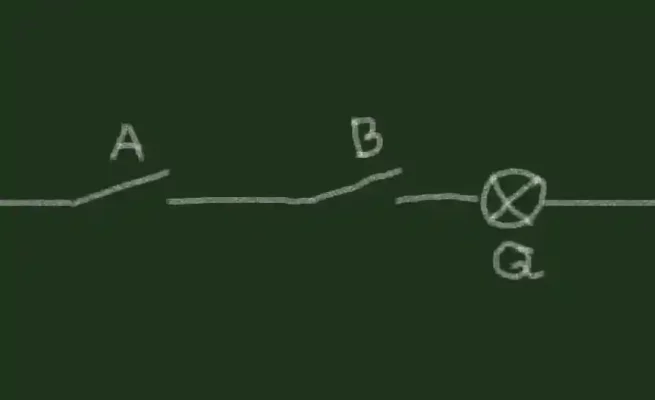
اولین راهی که می توانیم کلیدها و لامپ را به هم وصل کنیم این است که همه آنها را در یک خط مستقیم از خط خنثی وصل کنیم. به این می گویند سوئیچ ها را به صورت سری وصل کنید:

وقتی سوئیچ ها را به صورت سری قبل از لامپ وصل می کنیم، برای روشن شدن لامپ باید هر دو کلید روشن باشند. در منطق دیجیتال به آن گیت AND می گویند. چرا اینطور است؟ چون هم سوئیچ اول و هم سوئیچ دوم باید روشن باشند. در مثال واقعی ما، وضعیت کلیدها و لامپ روشن و خاموش است و در منطق دیجیتال دو حالت درست و نادرست است. به آن فکر کنید که سوئیچ ها و لامپ نشان دهنده حالت های درست و نادرست است. اگر روشن باشند درست و اگر خاموش باشند نادرست هستند.
منطق ترکیبی و شش گیت
حال، اجازه دهید به اصطلاح AND-gate برگردیم. AND-gate راهی برای تعیین وضعیت یک خروجی با دو ورودی به عنوان تصمیم است. این منطق ترکیبی نامیده می شود زیرا ما ورودی های بیشتری (متغیرهای جبر بولی) را با هم ترکیب می کنیم.
گیت AND
همه گیت ها در منطق ترکیبی دارای ورودی و خروجی هستند. سپس وضعیت خروجی توسط ورودی ها تعیین می شود. بنابراین با یک گیت AND هر دو ورودی و خروجی باید درست باشد. در مثال واقعی، دو سوئیچ ورودی و لامپ خروجی هستند. در منطق ترکیبی، وضعیت خروجی بلافاصله تصمیم گیری می شود. بنابراین، به محض اینکه ورودی ها وجود دارند، وضعیت خروجی تنظیم می شود. اگر هر دو سوئیچ را روشن کنیم لامپ روشن می شود.
AND-gate را می توان با نمادی مانند زیر ترسیم کرد:
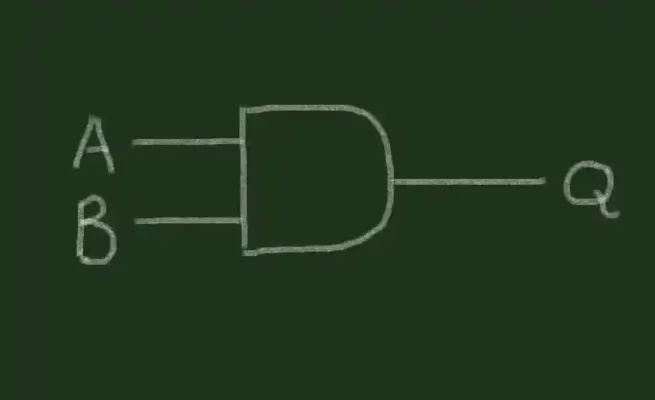
نام ها یا نمادهای استاندارد برای ورودی ها در منطق دیجیتال A و B وجد دارند. برای خروجی نماد استاندارد Q است. گیت هایی که در حال حاضر با آنها کار خواهیم کرد، همه دارای دو ورودی و یک خروجی هستند. هر گیت با تنظیم وضعیت خروجی عملکرد ساده ای را انجام می دهد. برخی از گیت ها ممکن است بیش از دو ورودی داشته باشند، اما همه گیت ها تنها یک خروجی خواهند داشت.
وضعیت ورودی ها و خروجی ها را می توان با جدول صدق نشان داد. برای هر گیت منطق ترکیبی، میتوانیم جدول صدق را برای توصیف عملکرد آن ترسیم کنیم.
جدول حقیقت برای AND-gate به شکل زیر خواهد بود:
| A • B |
A |
| false |
true |
| B |
false |
false |
false |
| true |
false |
true |
با این جدول می توانیم عملکرد و حالات خروجی را با هر ترکیب ممکنی از ورودی ها ببینیم.
محتوای فیلد بزرگ در گوشه سمت چپ بالا فرمول AND-gate است. گیت AND (A و B) باید به صورت: AB، A^B یا A • B نوشته شود.
فیلدهایی که با یک خط ضخیم مشخص شده اند، نتایج خروجی گیت AND هستند که با Q نمادین شده اند. دو فیلد زیر A و دو فیلد کنار B مقادیر ورودی های A و B هستند. مقادیر می توانند نادرست و درست باشند. اما برای اینکه کار را برای ما آسان تر کنیم، اجازه دهید درست و نادرست را با 0 و 1 تغییر دهیم. در اکثر PLC ها وضعیت ورودی ها و خروجی ها با 0 برای false و 1 برای true توصیف می شود.
در اینجا جدولی برای مقایسه نامها و اصطلاحات مختلف برای مثال واقعی ما، منطق ترکیبی، منطق دیجیتال و الکترونیک در PLC وجود دارد:
| Light switches |
Combinatorial logic |
PLC program logic |
PLC electronics |
| off |
false |
۰ |
0 volt |
| on |
true |
۱ |
5 volt |
اجازه دهید نگاهی به جدول حقیقت برای گیت AND بیندازیم، اما این بار با 0 و 1 برای نشان دادن حالات ورودی ها و خروجی ها:
| A • B |
A |
| ۰ |
۱ |
| B |
۰ |
۰ |
۰ |
| ۱ |
۰ |
۱ |
خروجی Q فقط 1 (درست) خواهد بود اگر هر دو ورودی A و B 1 (درست) باشند.
اکنون، این گیت ممکن است با تنها دو ورودی و یک خروجی ساده به نظر برسد، اما این AND-gate در واقع یک برنامه ساده PLC است. سعی کنید تصور کنید که A و B ورودی های یک PLC و Q یک خروجی در PLC هستند. یک برنامه PLC فقط یک یا چند گیت منطقی است. این در فصل بعدی، زمانی که برنامه نویسی واقعی PLC ها را شروع می کنیم، توضیح داده خواهد شد. نکته مهمی که اکنون باید فهمید این است که یک برنامه PLC یک قطعه منطق است – درست مانند گیت AND. برنامه PLC حالت های ورودی ها را (درست مانند گیت) به عنوان تصمیم گیری برای وضعیت خروجی (درست مانند گیت) می گیرد.
گیت های منطقی بیشتر
گیت OR
AND-gate تنها نوع گیت در منطق ترکیبی نیست. اگر با دو سوئیچ و لامپ به مثال واقعی خود برگردیم، میتوانیم آنها را به روش دیگری به هم وصل کنیم. این دو کلید را می توان قبل از لامپ ها به صورت “موازی” به یکدیگر متصل کرد. این باعث می شود سوئیچ ها به روش دیگری کار کنند. اجازه دهید نگاهی به شماتیک این اتصال “موازی” بیندازیم:
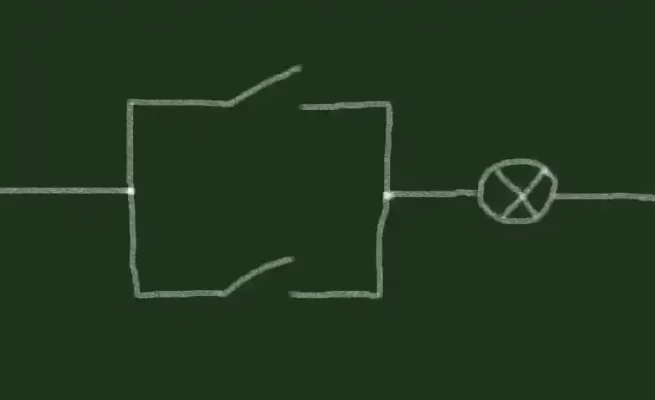
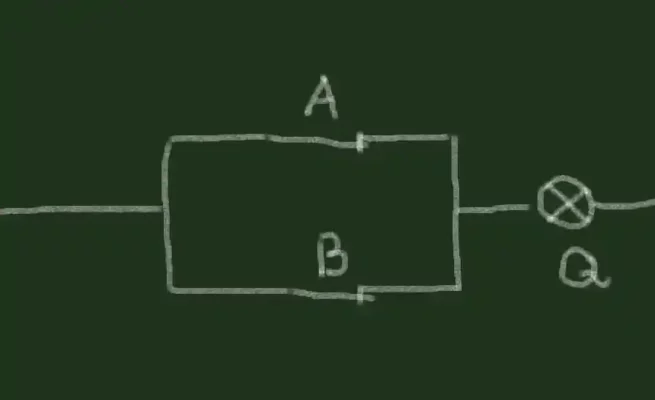
ما به این نوع اتصال، اتصال موازی می گوییم زیرا دو سوئیچ با یکدیگر موازی هستند. اتصال موازی کمی متفاوت از اتصال سریالی است که قبلاً استفاده می کردیم. اکنون که هر کلید مستقیماً با لامپ تماس دارد، هر کلید لامپ را روشن می کند. بنابراین برای روشن کردن لامپ باید سوئیچ اول یا کلید دوم روشن باشد. این عملکرد یک OR-gate است.
نماد گیت OR به شکل زیر است:
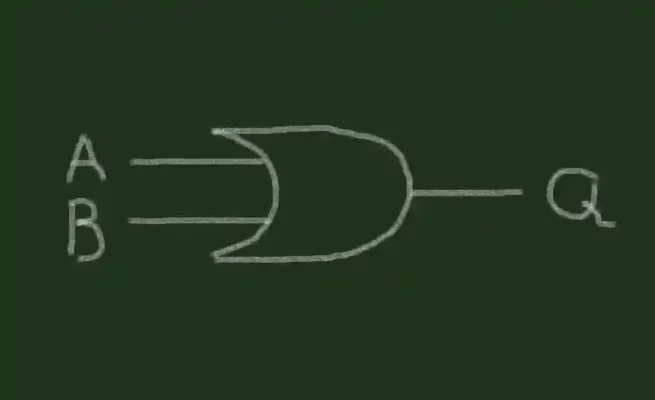
درست مانند AND-gate که قبلاً در مورد آن یاد گرفتیم، OR-gate دارای دو ورودی و یک خروجی است. نمادهای ورودی A و B و نماد خروجی Q است.
از آنجایی که گیت OR کمی متفاوت از AND-gate است، می توانیم یک جدول حقیقت جدید برای گیت OR ترسیم کنیم:
| A + B |
A |
| ۰ |
۱ |
| B |
۰ |
۰ |
۱ |
| ۱ |
۱ |
۱ |
همانطور که در فیلدهای مشخص شده با خطوط ضخیم می بینیم، خروجی گیت OR 1 (درست) خواهد بود اگر ورودی A یا ورودی B 1 (درست) باشند.
فرمول گیت OR به صورت A + B یا A ∨ B نوشته می شود.
هم گیت AND و هم گیت OR گیت های منطقی ساده ای هستند، زیرا توضیح آنها با دو سوئیچ و یک لامپ نسبتاً ساده است. دو سوئیچ نشان دهنده ورودی ها (A و B) و لامپ نشان دهنده خروجی (Q).
گیت NOT
در منطق ترکیبی 5 گیت وجود دارد که باید درباره آنها بدانیم، بنابراین با سه تا مانده، اجازه دهید به گیت بعدی برویم: گیت NOT. با AND-gate و OR-gate، این سه گیت، گیت های اصلی در منطق ترکیبی هستند. از این گیتها میتوانیم دو گیت دیگر را استخراج کنیم، اما ابتدا اجازه دهید نگاهی دقیقتر به NOT-gate بیندازیم:

NOT-gates خاص هستند زیرا خروجی با ورودی یکسان است. ورودی فقط به حالت مخالف معکوس می شود. به همین دلیل به آن NOT-gate می گویند. زیرا وقتی ورودی درست باشد، «خروجی» درست نیست، بلکه نادرست خواهد بود.
NOT-gate را اینورتر نیز می نامند زیرا مقدار ورودی (A) را می گیرد و آن را به حالت مخالف معکوس می کند. این را می توان با جدول حقیقت برای NOT-gate نشان داد. ممکن است متوجه شوید که جدول حقیقت برای NOT-gate کمی متفاوت از دو جدول صدق قبلی است که تاکنون به آنها نگاه کرده ایم:
مقادیر ستون اول زیر A حالت ورودی (A) و مقادیر ستون دوم زیر A مقادیر خروجی NOT-gate هستند. اما از آنجایی که ورودی و خروجی یکسان هستند، نمی توانیم در مورد خروجی ها با این گیت صحبت کنیم. NOT-gate واقعاً یک گیت نیست، زیرا هیچ تصمیمی نمی گیرد. فقط مقدار یک ورودی را تغییر می دهد.
فرمول NOT-gate به این صورت نوشته شده است: A، A’، ¬A و گاهی اوقات NOT A یا !A.
گیت های منطقی مشتق شده
با سه گیت ای که اکنون در مورد آنها می دانیم، دو گیت آخر را استخراج می کنیم. دو گیت آخر کمی پیچیده تر هستند. برای توضیح آنها، از نظر مثال واقعی ما با سوئیچ ها و لامپ، ما نیاز به گسترش عملکرد دو سوئیچ داریم. دو گیت بعدی کمی متفاوت از دو گیت اول کار می کنند، بنابراین نمی توانیم از مثال ساده فقط با دو سوئیچ استفاده کنیم. اگر نگاهی به گیت بعدی، گیت XOR بیندازیم، مشخص خواهد شد.
گیت XOR
XOR-gate همچنین گیت OR انحصاری نامیده می شود، زیرا عملکرد آن کمی شبیه گیت OR است اما با یک تفاوت اساسی. وقتی هر دو ورودی در یک گیت OR درست باشد، خروجی درست خواهد بود. اما وقتی هر دو ورودی در یک گیت XOR درست باشند، خروجی نادرست خواهد بود.
ابتدا به جدول حقیقت برای XOR-gate نگاهی بیندازید:
| A ⊕ B |
A |
| ۰ |
۱ |
| B |
۰ |
۰ |
۱ |
| ۱ |
۱ |
۰ |
به 0 زیر خط کشیده شده در گوشه پایین سمت راست جدول توجه کنید. این تفاوت بین گیت OR و گیت XOR است.
فرمول گیت XOR به صورت زیر نوشته شده است: A ⊕ B.
قبل از اینکه به مثال دنیای واقعی خود بپردازیم، بیایید سعی کنیم گیت XOR را با سه گیت اصلی در منطق ترکیبی بسازیم. به یاد داشته باشید که دو گیت آخر از جمله این گیت XOR را می توان با سه گیت اصلی مشتق کرد (ساخت).
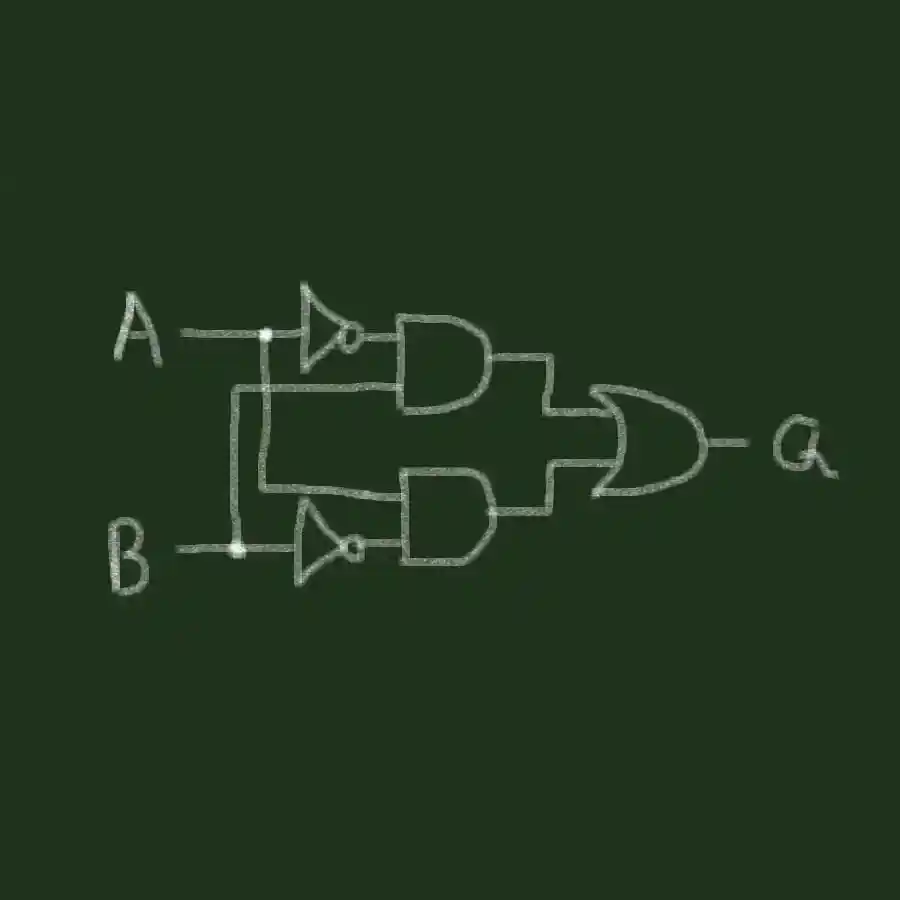
XOR-gate را می توان با استفاده از دو NOT-Gate دو AND-Gate و یک OR-Gate ساخته یا مشتق کرد:
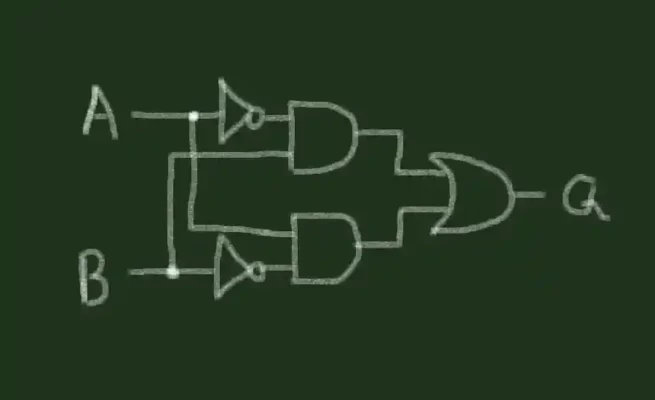
عملکرد پنج گیت ترکیبی معادل گیت XOR است. اگر ورودی A یا ورودی B 1 (درست) باشد، خروجی 1 (درست) خواهد بود، اما اگر هر دو ورودی 1 (درست) باشند، نه.
به طور معمول باز و به طور معمول بسته است
با بازگشت به مثال واقعی خود، اکنون می توانیم عملکرد دو سوییچ را گسترش دهیم.
سوئیچ ها می توانند به دو روش مختلف کار کنند: با ایجاد یک اتصال یا با قطع اتصال. این دو روش عملکرد معمولاً باز و معمولاً بسته نامیده می شوند. نام ها با وضعیت پیش فرض مخاطبین در سوئیچ تعریف می شوند. اگر مخاطب “باز” باشد و ارتباط برقرار نکند، به آن یک تماس معمولی باز یا یک تماس NO می گویند. کنتاکت معمولاً باز به شکل زیر ترسیم می شود:

مخاطب دیگر، تماس معمولی بسته نامیده میشود، زیرا حالت پیشفرض مخاطب یک اتصال را ایجاد میکند. تماس معمولی بسته یا NC-contact با این نماد رسم می شود:

یک سوئیچ می تواند بیش از یک کنتاکت داشته باشد. وجود دو کنتاکت در یک سوئیچ غیرعادی نیست، جایی که یکی از آنها به طور معمول باز و دیگری به طور معمول بسته است. این به سوئیچ دو عملکرد می دهد: یک عملکرد ساخت و یک عملکرد شکست.
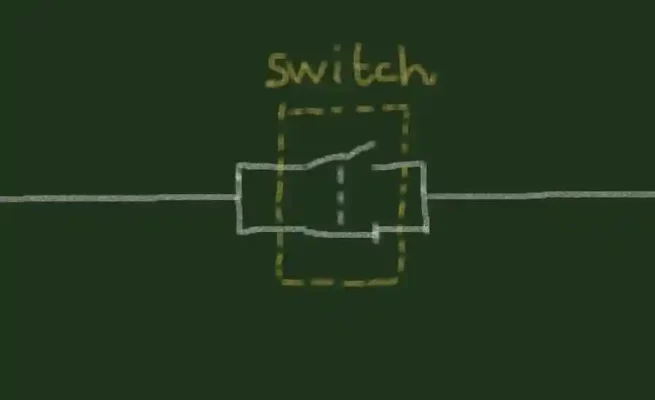
هنگامی که سوئیچ بالا فعال می شود، NO-contact یک اتصال برقرار می کند و NC-contact اتصال را قطع یا قطع می کند. تمام کنتاکت های داخل سوئیچ همزمان با فعال شدن سوئیچ فعال می شوند.
برای نشان دادن دو گیت اول، OR-gate و AND-gate ما از کنتاکت های معمولی باز در سوئیچ های خود استفاده کردیم. این بدان معنی است که وقتی سوئیچ ها را فعال می کنیم یک اتصال برقرار می شود. اما برای نشان دادن گیت XOR با مثال دنیای واقعی ما باید از NC-contact نیز استفاده کنیم. چرا؟ زیرا NC-contact ها همان NOT-gate هستند.
در مورد آن فکر کنید. NOT-gate سیگنال ورودی را معکوس می کند و همین امر در مورد NC-contact صدق می کند. اگر جدول حقیقت را برای NC-contact رسم کنیم، واضح تر خواهد بود:
| NC – IN |
NC – OUT |
| OFF – 0 _.__._ |
ON – 1 |
| ON – 1 _./ ._ |
OFF – 0 |
این جدول حقیقت دقیقاً شبیه جدول حقیقت NOT-gate است. هنگامی که NC-contact خاموش است یا در حالت پیش فرض خود قرار دارد، مخاطب اتصال را برقرار می کند و خروجی مخاطب روشن یا 1 (درست) خواهد بود. و اگر NC-contact فعال باشد یا در حالت true یا 1 باشد خروجی 0 یا false خواهد بود. کنتاکت معمولاً بسته همان کار گیت NOT را انجام می دهد: معکوس کردن سیگنال به حالت مخالف.
این به ما می دهد سه قانون را دنبال کنیم:
- مخاطبین سریال همان AND-gates هستند.
کنتاکت های موازی همان گیت های OR هستند.
NC-contact ها همان NOT-gates هستند.
بنابراین، چگونه می توانیم سوئیچ ها و لامپ خود را برای نشان دادن گیت XOR متصل کنیم؟ ابتدا باید به اتصالاتی که برای گیت OR ایجاد کردیم نگاهی بیندازیم:
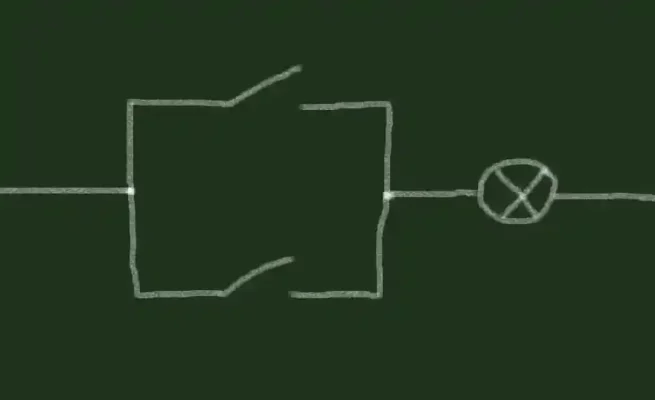
این به خوبی کار می کند، اما تفاوت بین OR-gate و XOR-gate را به خاطر دارید؟ وقتی هر دو کنتاکت در گیت OR فعال می شوند، لامپ روشن است، اما با گیت XOR، لامپ باید خاموش باشد. بنابراین، برای ساختن گیت XOR، باید از روشن شدن لامپ هنگام فعال شدن هر دو کنتاکت جلوگیری کنیم.
با یادآوری اینکه گیت OR معادل یک مدار موازی است، اجازه دهید سعی کنیم از یک کنتاکت معمولی بسته در یکی از سوئیچ ها استفاده کنیم. این مخاطب جدید می تواند به روش های مختلف به اتصال موازی ما متصل شود. ابتدا میتوانیم آن را به موازات دو مخاطب دیگر وصل کنیم:
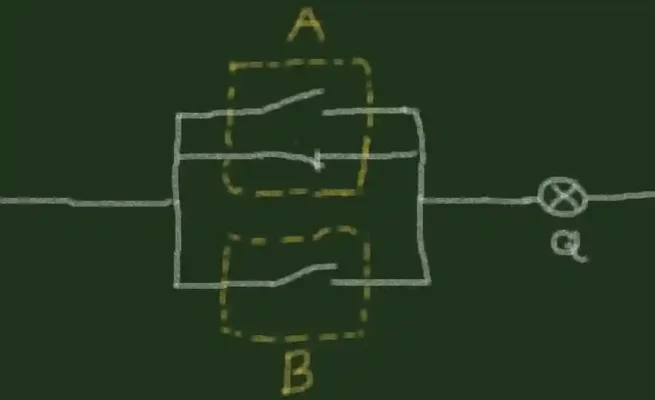
با این حال، این هیچ منطقی نخواهد داشت، زیرا لامپ اکنون همیشه روشن است. به جدول حقیقت نگاه کنید:
| Switches A and B |
A |
| OFF |
ON |
| B |
OFF |
ON |
ON |
| ON |
ON |
ON |
مهم نیست که سوئیچ ها روشن یا خاموش باشند، لامپ همیشه روشن خواهد بود.
از آنجایی که کار نکرد، اجازه دهید سعی کنیم NC-contact جدید را به روشی متفاوت متصل کنیم:
اتصال سریال تماس معمولی بسته جدید
اکنون سوئیچ اول دارای دو عملکرد یا دو کنتاکت است. یکی برای ایجاد ارتباط و یکی برای قطع ارتباط. اگر نگاهی به جدول حقیقت مدار جدید خود بین کنتاکت های سوئیچ ها و لامپ بیندازیم، ممکن است متوجه شوید که عملکرد مانند گیت OR است:
| Switches A and B |
A |
| OFF |
ON |
| B |
OFF |
OFF |
ON |
| ON |
ON |
ON |
NC-contact جدید هیچ تفاوتی ایجاد نکرد. اما اگر هر دو سوئیچ دو عملکرد داشته باشند چه می شود. مرحله بعدی استفاده از هر دو کنتاکت معمولی باز و بسته معمولی در دو سوئیچ خواهد بود.
اما این بار از سه قانون ذکر شده در بالا استفاده خواهیم کرد. ما باید از قوانین استفاده کنیم، زیرا می توانیم کنتاکت ها و لامپ را به روش های مختلف وصل کنیم. البته ما فقط میتوانیم حدس بزنیم که چگونه باید مخاطبین را به هم متصل کنیم تا یک گیت XOR بسازیم. اما زمانی که از قوانین پیروی می کنیم، باید زمان کمتری برای استخراج XOR-gate طول بکشد.
از آنجایی که ما از قبل یک گیت OR داریم، می توانیم قانون اول را اعمال کنیم: اتصال موازی گیت OR است. ما قبلاً ارتباط موازی با مخاطبین معمولی باز داریم، بنابراین این گیت OR را تشکیل می دهد. اما از آنجایی که در صورت فعال شدن هر دو سوییچ (ورودی) خروجی باید NOT درست باشد، ممکن است به ما بگوید که باید از برخی NOT-Gates استفاده کنیم. این دومین قاعده ای است که از آن استفاده خواهیم کرد: گیت های NOT کنتاکت های معمولا بسته هستند. ما باید برخی از NC-contactها را در مثالی در دنیای واقعی وارد کنیم.
اگر هر دو سوئیچ فعال شوند، لامپ نباید فعال شود، بنابراین ممکن است یک کنتاکت معمولی بسته را از هر سوئیچ در مثال خود وارد کنیم.
چیزی که اکنون داریم یک گیت OR است و چیزی که نیاز داریم این است که هر دو اتصال به لامپ را با فعال شدن هر دو کلید قطع کنیم. ما باید هر دو اتصال یا ورودی به لامپ را قطع کنیم، زیرا اگر فقط یکی از ورودیهای یک گیت OR درست باشد، گیت درست خواهد بود. این را می توان با اتصال کنتاکت های معمولی بسته سوئیچ ها در اتصال سریال به کنتاکت معمولی باز روی کلید دیگر انجام داد:
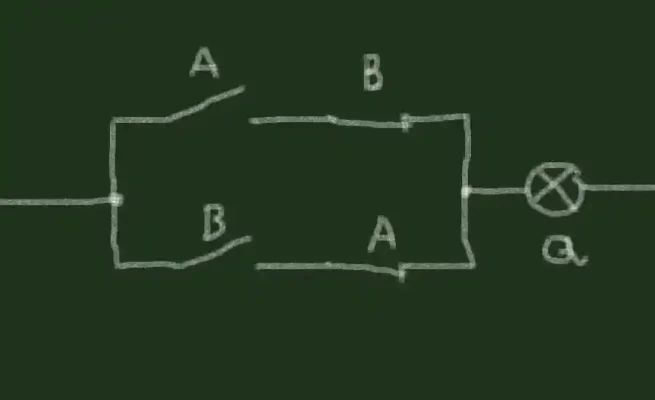
با نگاه کردن به جدول حقیقت برای این مدار، خواهیم دید که اکنون یک گیت XOR ساخته ایم. درست مانند گیت OR کار می کند، اما با یک تفاوت که وقتی هر دو سوئیچ فعال می شوند، لامپ روشن نمی شود.
| A ⊕ B |
A |
| ۰ |
۱ |
| B |
۰ |
۰ |
۱ |
| ۱ |
۱ |
۰ |
با توضیح چهار گیت، اکنون تنها دو گیت باقی مانده است. دو گیت آخر مخالف دو گیت اول یا نسخه های وارونه دو گیت اول هستند. این بدان معناست که خروجی مقدار مخالف یا معکوس با همان حالت ورودی دو مورد اول خواهد بود. دو گیت آخر NOR-gate و NAND-gate نامیده می شوند.
گیت NOR
NOR-gate و NAND-gate متضاد گیت OR و AND-gate است. آنها معکوس هستند زیرا “N” که در جلوی نام ها قرار می دهیم مخفف NOT است. NOR-gate گیت NOT OR و NAND-gate NOT AND-gate است.
ابتدا به جدول حقیقت برای گیت NOR نگاهی بیندازید. گیت NOR، گیت OR معکوس است:
| A NOR B |
A |
| ۰ |
۱ |
| B |
۰ |
۱ |
۰ |
| ۱ |
۰ |
۰ |
اگر به حالتهای خروجی که با خطوط ضخیم مشخص شدهاند نگاه کنید، همه آنها دقیقاً برعکس گیت OR هستند. به همین دلیل است که به آن NOT OR-gate می گویند. هنگامی که ما در حال استخراج یا ساختن گیت NOR با سه گیت اصلی هستیم، این نام نیز معنا پیدا می کند. NOR-gate از OR-gate و NOT-gate مشتق شده است. NOT-gate خروجی OR-gate را معکوس می کند که به ما گیت OR معکوس می دهد که به نام NOR-gate نیز شناخته می شود.
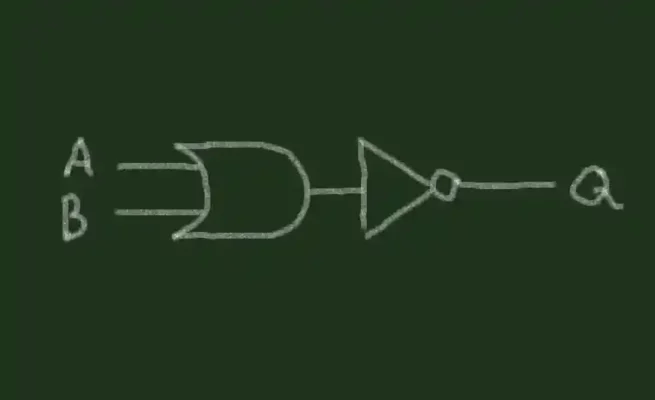
همان اصل استخراج گیت مقابل هنگام استخراج آخرین گیت از شش گیت در منطق ترکیبی – گیت NAND – اتفاق می افتد.
گیت NAND
گیت NAND برعکس گیت AND است و NOT AND-gate نیز نامیده می شود. NAND-gate از AND-gate و NOT-gate به همان شیوه NOR-gate مشتق شده است. NOT-gate خروجی AND-gate را معکوس می کند که برعکس گیت AND – NAND-gate را می سازد.
هر دو گیت NAND و NOR-gate را می توان در مثال دنیای واقعی با دو سوئیچ که ورودی ها و لامپ را نشان دهنده خروجی نشان می دهد، نشان داد. برای انجام این کار، باید نگاهی به جداول حقیقت بیندازیم.
در اینجا جدول حقیقت برای NAND-gate آمده است:
| A NAND B |
A |
| ۰ |
۱ |
| B |
۰ |
۱ |
۱ |
| ۱ |
۱ |
۰ |
همانطور که در جدول صدق می بینید، خروجی همیشه 1 (true) است به جز زمانی که هر دو ورودی 1 (true) باشند. این به این معنی است که حتی زمانی که هر دو ورودی 0 (نادرست) باشند، خروجی 1 (درست) خواهد بود. با در نظر گرفتن این موضوع، اکنون می دانیم که باید از کنتاکت های معمولی بسته (NC) در سوئیچ های خود استفاده کنیم. آنها لامپ را روشن می کنند (درست) وقتی خاموش هستند (نادرست).
اکنون یک چیز جالب می آید که منجر به بخش پیشرفته تری از منطق ترکیبی یا جبر بولی می شود. به یاد داشته باشید که یکی از قوانین می گوید که یک اتصال موازی یک OR-gate است. این تنها زمانی صادق است که ورودی ها معکوس نباشند. زیرا هنگامی که در حال نشان دادن NAND-gate با سوئیچ ها هستیم، دو سوئیچ به صورت موازی به یکدیگر متصل می شوند:
وقتی ورودیها را معکوس میکنیم (در مثال ما: استفاده از کنتاکتهای معمولی بسته به جای معمولی باز)، اتصال موازی یک NAND-gate میسازد. شرح آنچه هنگام معکوس شدن ورودی ها اتفاق می افتد، قضیه دمورگان نامیده می شود.
قضیه دمورگان هنگامی که ما گیت NOR را نشان می دهیم نیز کاربرد دارد. گیت NOR در مثال ما دو سوئیچ در اتصال سریال قبل از لامپ است. از آنجایی که NOR-gate یک گیت معکوس است، از کنتاکت های معمولی بسته استفاده می کنیم. این نیز یکی از قوانین را زیر پا می گذارد. قانونی که می گوید اتصالات سریال AND-gates هستند. اتصال سریال فقط زمانی است که از مخاطبین باز استفاده می کنیم. هنگامی که کنتاکت ها به طور معمول بسته هستند، نشان می دهد که ورودی ها معکوس هستند، اتصال سریال NOR-gate خواهد بود.
ساده ترین راه برای استخراج NOR-gate و NAND-gate این است که ورودی ها را معکوس کنیم. در مثال ما به عنوان استفاده از کنتاکت های بسته به طور معمول نشان دهنده ورودی های معکوس نشان داده شده است. اما زمانی که ما NOR-gate و NAND-gate را با استفاده از گیت های اصلی استخراج کردیم، خروجی را معکوس می کردیم و نه ورودی ها را.
بیایید سعی کنیم با معکوس کردن ورودی های یک گیت OR، NOR-gate را استخراج کنیم:
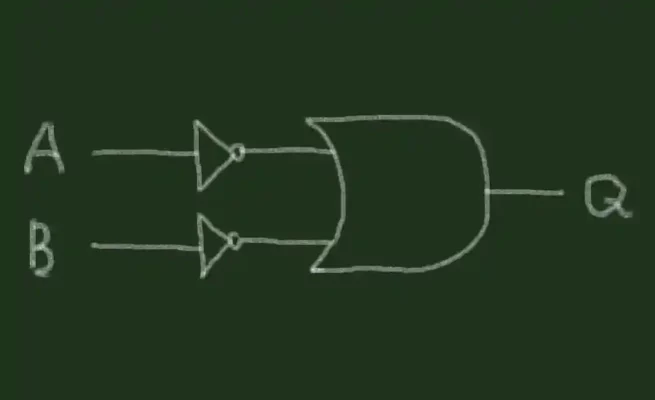
این همان جدول حقیقت را دارد که اگر خروجی یک گیت OR را معکوس کنیم. دقیقاً همین اتفاق می افتد اگر سیگنال های ورودی یک AND-gate را معکوس کنیم تا یک NAND-gate بسازیم. از این مشاهدات می توان قانون دیگری را بیان کرد:
معکوس کردن ورودی ها یا معکوس کردن خروجی ها همین تأثیر را روی عملکرد دارد.
در نهایت، اجازه دهید سعی کنیم خروجی ها را در مثال دنیای واقعی خود معکوس کنیم و ببینیم که آیا می توانیم گیت NAND و گیت NOR را نشان دهیم. در مثال ما لامپ نشان دهنده خروجی است. این بدان معنی است که ما باید عملکرد لامپ را معکوس کنیم. اما چگونه؟
جواب رله است. رله ها مجموعه ای از کنتاکت ها هستند که با هم در یک ظرف کوچک ساخته می شوند. رله درست مانند لامپ با برق فعال می شود. اما هنگامی که رله فعال می شود تمام کنتاکت های آن نیز فعال می شوند. رله درست مانند سوئیچ های ما است، اما به جای دستی، کنتاکت ها به صورت الکتریکی فعال می شوند.
برای معکوس کردن خروجی باید به جای لامپ یک رله قرار دهیم. حالا خروجی به جای لامپ، رله را فعال می کند:
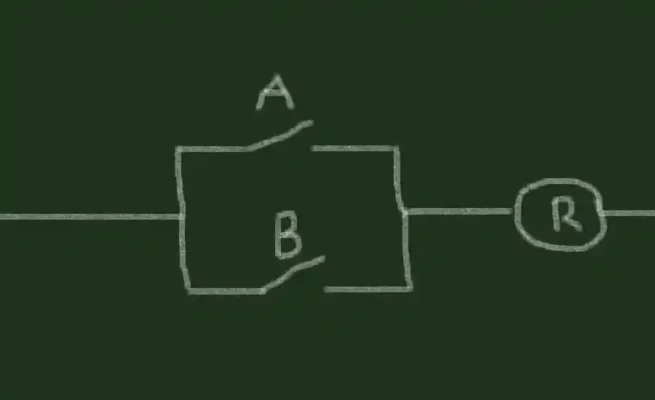
برای معکوس کردن خروجی همچنان به لامپ نیاز داریم، بنابراین با ایجاد یک اتصال جدید بین لامپ و یکی از کنتاکت های رله، اکنون می توانیم لامپ را با رله فعال کنیم. اما برای اینکه رله لامپ را برعکس فعال کند (خروجی معکوس) باید از یک کنتاکت معمولی بسته در رله استفاده کنیم. این خروجی و در نتیجه لامپ ما را معکوس می کند:
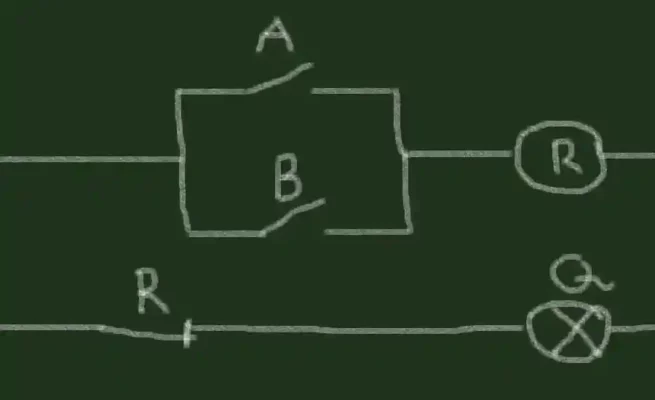
این معکوس کردن خروجی در یک اتصال موازی به ما گیت NAND می دهد. می توانیم خروجی اتصال سریال را با یک رله نیز معکوس کنیم و NOR-gate را دریافت کنیم.
با تمام گیتهای نشاندادهشده، اکنون دانش پایهای از شش گیت در منطق ترکیبی داریم:
- گیت AND
- گیت OR
- گیت NOT
- گیت XOR
- گیت NAND
- گیت NOR